今回は、scikit-learnというPython機械学習ライブラリを使って、クラスタリング(クラスター分析)を試してみます。
クラスタリングとは?
クラスタリングとは、大きな集団の中から似たもの同士を集めて、グループに分けることをいいます。
しかし、性別や年齢など、わかりやすい判断基準の集団に分けるのは、クラスタリングとは呼べません。
クラスタリングは、1つの大きなデータを近しいデータ毎に各クラスター(房(ふさ)や、群れ、集団という意味)に分けたのち、そのクラスターにどんな意味があるのかを人間が意味づけをしていきます。
なにはともあれ、さっそくScikit-learnを使ってプログラムを実装していきましょう。
クラスタリングを試してみよう – データを作る
以下、店舗などのサイトがあるとして、架空のデータを作ります。
まず、今回の分析したい目標をふんわり決めます。
「店舗のサイトに訪れる客層を知りたい」にしましょう。
目標が決まったので、次にデータを作成します。今回のデータ収集方法は、簡単なアンケートです。
合計として、約1000人のデータを集めたとします。また、解答欄には「フリー記入欄」なく、全て選択式です。
アンケート項目は以下です。
Q1:1日にどれぐらいネットをご利用になりますか?
- 1日5時間以上
- 1日3時間以上
- 1日1時間以上
- 1日1時間未満
Q2:普段、雑誌などは読まれますか?
- 1年に1冊以上
- 1ヶ月に1冊以上
- 1週間に1冊以上
- 1日1冊以上
- まったく読まない
Q3:一日にテレビはどれくらい見られますか?
- 1日5時間以上
- 1日3時間以上
- 1日1時間以上
- 1日1時間未満
- まったく見ない
Q4:普段よく使う移動手段はなんですか?
- 電車
- バス
- 徒歩
- 自転車
- オートバイ
- 自動車
Q5:普段からよく使っているものはいつ買ったものですか?
- ここ1週間
- 1ヶ月以内
- 半年以内
- 1年以内
- 3年未満
- 3年以上前
Q6:常に最新のトレンドを知っていないと落ち着かないですか?
- まったくそう思わない
- 少し思う
- 普通
- すごく思う
Q7:趣味はありますか?
- 趣味はない
- ゲーム、ネット、コンピュータ系
- 読書
- 動画、映像を見る
- 音楽
- アウトドア全般
- ファッション全般
- 旅行、レジャー全般
- スポーツ全般
Q8:どのような家族構成ですか?
- 答えたくない
- 兄がいる
- 姉がいる
- 弟がいる
- 妹がいる
- 1人っ子
Q9:外によく買い物にいくほうですか?
- 1日1回以上はいく
- 週に2〜3回程度
- 1ヶ月に4〜5回程度
- ほとんどネットショッピングで済ませる
- 1年に数回
Q10:興味があることに費やす時間はどれくらいですか?
- 1日5時間以上
- 1日3時間以上
- 1日1時間以上
- 1日1時間未満
- まったくしてない
内容は適当です。
思いついたことを約10問にまとめました。
次にクラスタリングしやすいようにアンケートの回答を数値化します。
単純に回答の数字とします。
それでは、プログラミングしていきましょう。
import numpy as npcol=[‘ネット時間’,’雑誌時間’,’テレビ時間’,’移動手段’,’購入頻度’,’トレンド’,’趣味’,’家族構成’,’買い物’,’興味’]row=[]for _ in range(1000):
web=np.random.randint(1,5)
magazin=np.random.randint(1,6)
tv=np.random.randint(1,6)
trans=np.random.randint(1,7)
tool=np.random.randint(1,7)
trend=np.random.randint(1,5)
hobby=np.random.randint(1,10)
family=np.random.randint(1,7)
outside=np.random.randint(1,6)
intrests=np.random.randint(1,6)row.append(np.array([web,magazin,tv,trans,tool,trend,hobby,family,outside,intrests]))
features=pd.DataFrame(row,columns=col)
アンケートの質問を簡単にして列名にし、回答をnumpyのランダムを使って行にします。
1,000回、行を作って変数rowに格納していきます。
最後にpandasのデータフレームを作成します。
確認してみましょう。
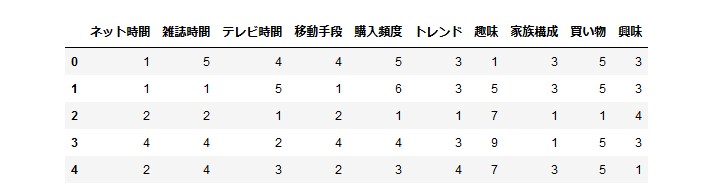
回答はランダムな数字になっているようです。
クラスタリングを試す
続いて本題のScikit-learnによるクラスタリングです。
今回はクラスタリングにおいて、よく使われているK-means法を使います。
以下をインポートしてください。
Kmeans法を使うのはとても簡単です。
これでクラスター分けができました。
確認してみましょう。
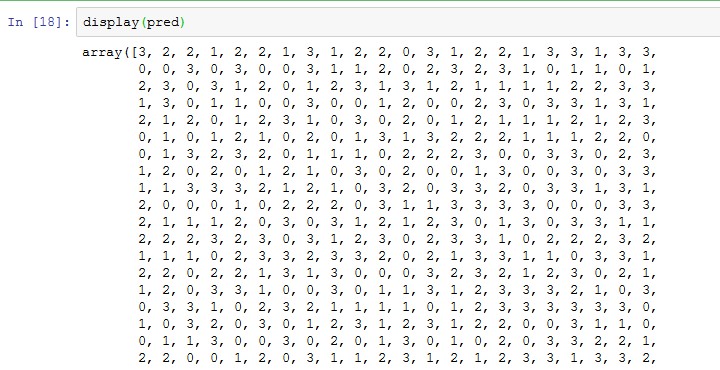
うまく分けられているようです。
詳細を確認します
詳細を確認してみましょう。
pred features[‘cluster_id’].value_counts()
クラスターIDを学習用データフレームにくっつけます。
そして、value_counts()メソッドで数を確認します。
だいたい、同じくらいの数に分けられています。
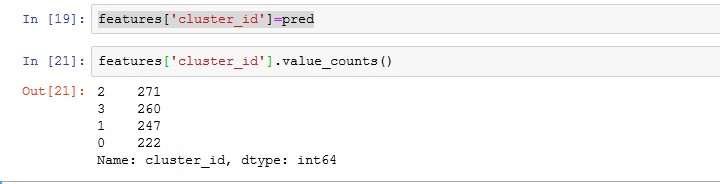
各クラスターごとの平均値などを見ていきましょう。
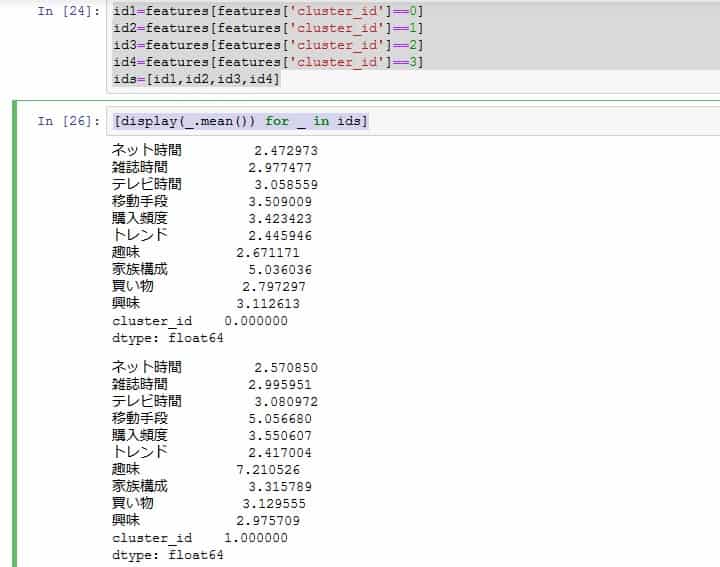
さて、ここで疑問です。
本当にこのクラスター数でいいのでしょうか。
結果がいまいちのとき、どうしたら次に考える最適なクラスター数を求めるのでしょうか。
それを調べる方法として、エルボー法とシルエット法があります。
まず、エルボー法で調べてみましょう。
エルボー法を試してみる
https://qiita.com/deaikei/items/11a10fde5bb47a2cf2c2
こちらのサイトを参考にしてコードを作成してみました。
%matplotlib inlinedistortions = []for i in range(1,11): # 1~10クラスタまで一気に計算
km = KMeans(n_clusters=i,
init=’k-means++’, # k-means++法によりクラスタ中心を選択
n_init=10,
max_iter=300,
random_state=0)
km.fit(features) # クラスタリングの計算を実行
distortions.append(km.inertia_) # km.fitするとkm.inertia_が得られるplt.plot(range(1,11),distortions,marker=’o’)
plt.xlabel(‘Number of clusters’)
plt.ylabel(‘Distortion’)
plt.show()
ガクンと角度が変わるところに注目です。
この肘のような形になることからエルボー法と呼ばれてます。
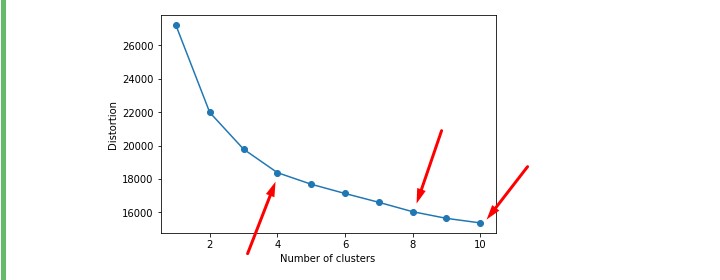
さて、どうやら矢印の場所らへんが怪しそうです。
4は試したので、8にしてみましょう。
あまりクラスターを分けすぎると判断がしづらくなります。
features[‘cluster_id’]=pred
features[‘cluster_id’].value_counts()
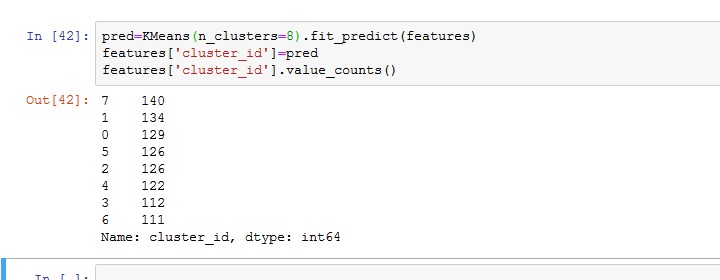
シルエット法を試してみる
続いてシルエット法です。
簡単に説明すると、下のような図になっていて、
クラスター=8
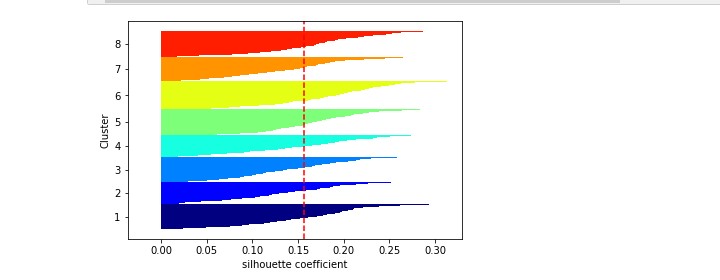
すべてのラインが赤い線を超えていて、すべてのラインの太さが均一であれば最適であろうとされています。
from matplotlib import cmkm = KMeans(n_clusters=8, # クラスターの個数
init=’k-means++’, # セントロイドの初期値をランダムに設定
n_init=10, # 異なるセントロイドの初期値を用いたk-meansあるゴリmズムの実行回数
max_iter=300, # k-meansアルゴリズムの内部の最大イテレーション回数
tol=1e-04, # 収束と判定するための相対的な許容誤差
random_state=0) # セントロイドの初期化に用いる乱数発生器の状態
y_km = km.fit_predict(features)cluster_labels = np.unique(y_km) # y_kmの要素の中で重複を無くす
n_clusters=cluster_labels.shape[0] # 配列の長さを返す。つまりここでは n_clustersで指定した3となる# シルエット係数を計算
silhouette_vals = silhouette_samples(features,y_km,metric=’euclidean’) # サンプルデータ, クラスター番号、ユークリッド距離でシルエット係数計算
y_ax_lower, y_ax_upper= 0,0
yticks = []for i,c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km==c] # cluster_labelsには 0,1,2が入っている (enumerateなのでiにも0,1,2が入ってる(たまたま))
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals) # サンプルの個数をクラスターごとに足し上げてy軸の最大値を決定
color = cm.jet(float(i)/n_clusters) # 色の値を作る
plt.barh(range(y_ax_lower,y_ax_upper), # 水平の棒グラフのを描画(底辺の範囲を指定)
c_silhouette_vals, # 棒の幅(1サンプルを表す)
height=1.0, # 棒の高さ
edgecolor=’none’, # 棒の端の色
color=color) # 棒の色
yticks.append((y_ax_lower+y_ax_upper)/2) # クラスタラベルの表示位置を追加
y_ax_lower += len(c_silhouette_vals) # 底辺の値に棒の幅を追加silhouette_avg = np.mean(silhouette_vals) # シルエット係数の平均値
plt.axvline(silhouette_avg,color=”red”,linestyle=”–“) # 係数の平均値に破線を引く
plt.yticks(yticks,cluster_labels + 1) # クラスタレベルを表示
plt.ylabel(‘Cluster’)
plt.xlabel(‘silhouette coefficient’)
plt.show()
4個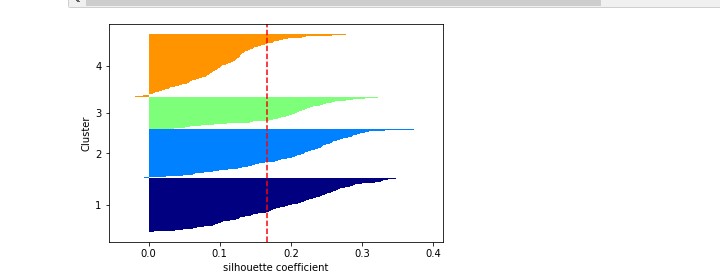
12個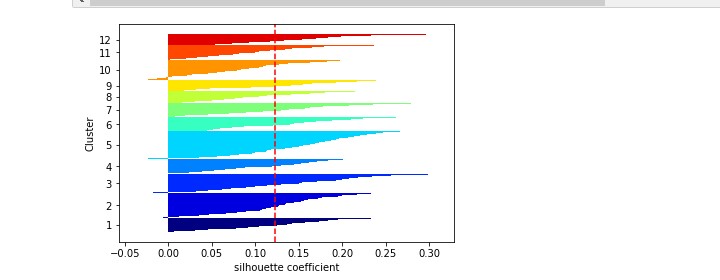
今回は8個にします。
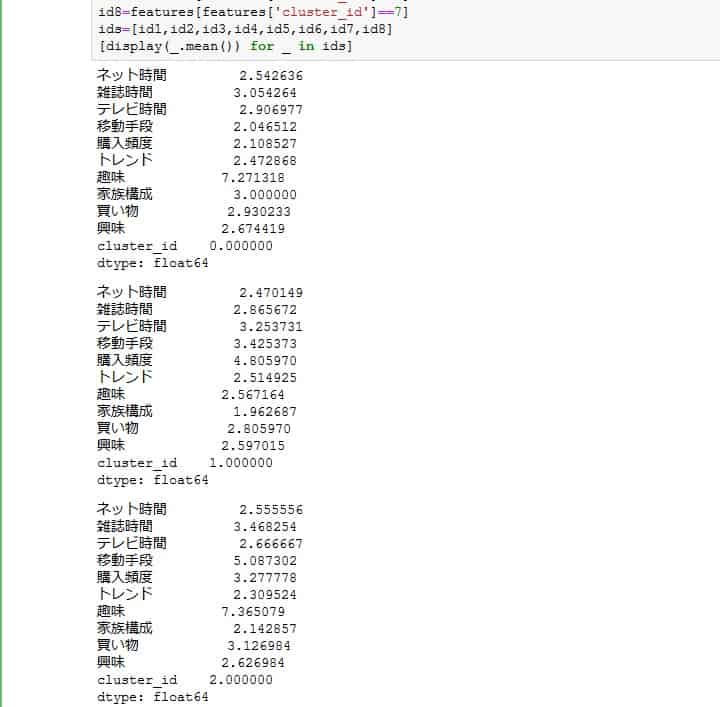
趣味の平均値が大きく離れています。
数字が小さいほどインドア派、大きいほどアウトドア派とざっくり分けます。
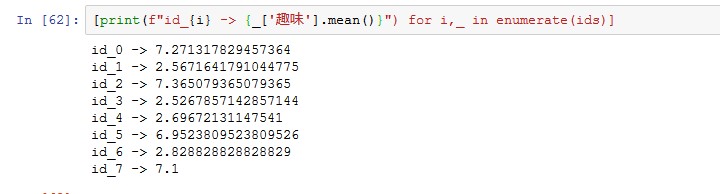
クラスターIDの、0,2,5,7と、1,3,4,6を分けます。
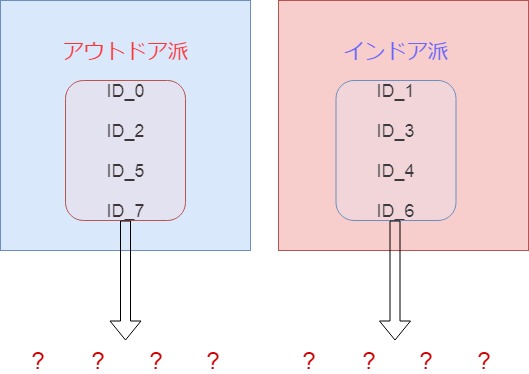
このように分けていき、あとは細かい分析をしていきます。
まとめ
Scikit-learnを使えば、たった2〜3行でクラスタリングができてしまいます。
皆様も、会社のデータなどを入れて試してみてください!
K-meansクラスタリングも学べる「ビジネス向けAI講習」も開催中です!
プログラミング経験が無い方でも受講できます。