現在のAIブームで注目されているニューラルネットワークでは、活性化関数という関数が用いられます。
本記事では、ニューラルネットワークで使われる代表的な活性化関数を紹介します。
ニューラルネットワークにおける活性化関数
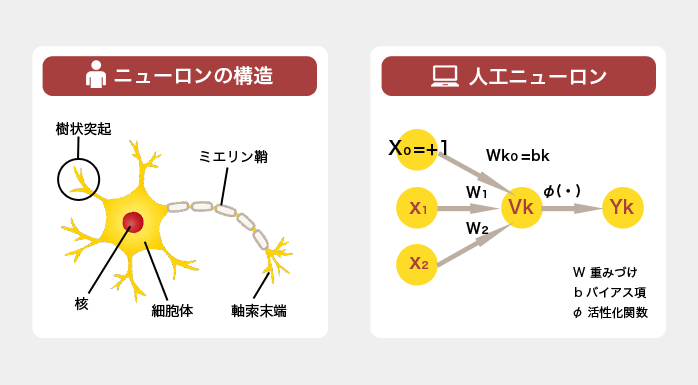
ニューラルネットワークは、人間の脳の神経細胞(ニューロン)を電気信号が伝わっていく様子を模倣したものです。
そのことから、ニューラルネットワークの最小単位は人工ニューロン(neuron)と呼ばれます。
ニューロンにおける入力に重みを乗算し、バイアスを加えた総和から出力を決定する関数のことを活性化関数と言います。
活性化関数は、ニューロンへのすべての入力を出力に変換する関数で、出力を決定するための非線形変換を担います。
活性化関数にはどんなものがあるか詳しく見ていきましょう。
AI(人工知能)用語集の中の活性化関数はこちら
本記事では関数のグラフを描くコードも載せておきます。
活性化関数
- ステップ関数
- シグモイド関数
- ReLU関数
- ソフトマックス関数
- 恒等関数
活性化関数①ステップ関数
まずは基本的なステップ関数です。
これは、単純パーセプトロンと全く同じものになります。
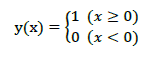
グラフは以下のようになります。
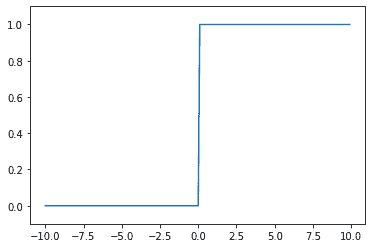
Pythonでグラフを描くコードは、以下のようになります。
import numpy as np
import matplotlib.pyplot as plt
def step_function(x):
y = x > 0
return y.astype(np.int)
x = np.arange(-10.0, 10.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
活性化関数②シグモイド関数
シグモイド関数は、あらゆる入力値を0~1の範囲の数値に変換して出力する関数です。
ニューラルネットワークでよく用いられてきた関数です。
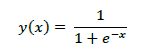
しかし、シグモイド関数を用いると勾配消失問題が起きやすく、学習が停滞してしまうことがあるため最近ではあまり用いられません。
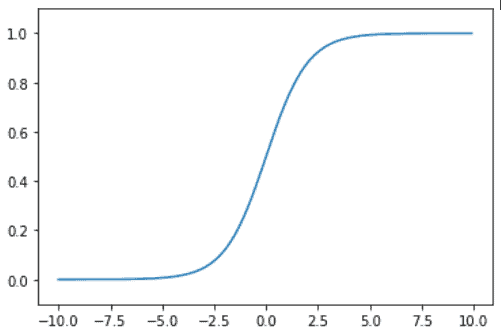
グラフを描くコードは、以下のようになります。
import numpy as np
import matplotlib.pyplot as plt
def sigmoid_function(x):
return 1 / (1 + np.exp(-x))
input_data = np.arange(-10.0, 10.0, 0.1)
output_data = sigmoid_function(input_data)
plt.plot(input_data, output_data)
plt.ylim(-0.1, 1.1)
plt.show()
活性化関数③ReLU関数
ニューラルネットワークでシグモイド関数の次に用いられてきたのが、ReLU関数です。
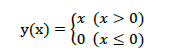
ReLU関数は勾配消失問題が起きにくく、形が簡単なので計算しやすいという特徴があります。
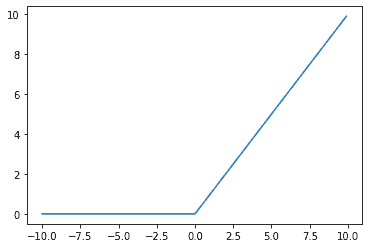 グラフを描くコードは以下のようになります。
グラフを描くコードは以下のようになります。
import numpy as np
import matplotlib.pyplot as plt
def relu(x):
return np.maximum(0, x)
x = np.arange(-10.0, 10.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.show()
活性化関数④ソフトマックス関数
ソフトマックス関数は、ニューラルネットワークにおいて分類問題の出力層で用いられます。
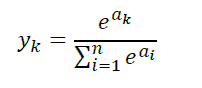
ソフトマックス関数は出力の総和は1になるという特徴があります。
グラフは以下のようになります。
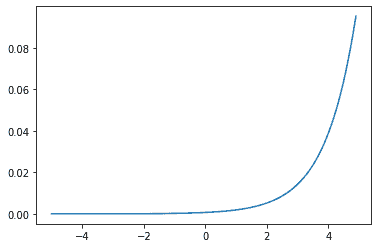
コードで確認してみます。
import numpy as np
import matplotlib.pyplot as plt
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
#a = np.array([0.3, 2.9, 4.0])
a = np.array([0.5, 3.1, 4.3])
y = softmax(a)
print(y)
print(np.sum(y))
#合計は1になる
x = np.arange(-5.0,5.0, 0.1)
y = softmax(x)
plt.plot(x, y)
plt.show()
実行結果は、 [0.01690191 0.22756284 0.75553525] 1.0 となります。
活性化関数⑤恒等関数
出力層で用いられる関数には、恒等関数もあります。
常に入力した値と同じ値をそのまま返す関数です。
この関数は、一般的に回帰問題で用いられます。
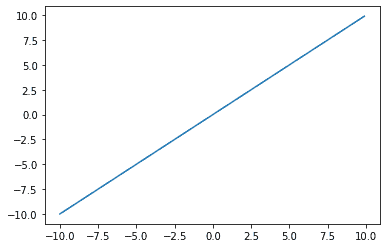
コードは以下のようになります。
import numpy as np
import matplotlib.pylab as plt
def identity(a):
return a
x = np.arange(-10.0, 10.0, 0.1)
y = identity(x)
plt.plot(x, y)
plt.show()最近の活性化関数
ReLU関数の後継として提案された、Swish関数とMish関数について紹介していきます。
- Swish関数
- Mish関数
最近の活性化関数①Swish関数
Swish関数は、2017年に提案されたReLU関数によく似た形の関数です。
しかし、x=0でも連続な関数となるところが違いになります。
Swish関数は以下のように表されます。
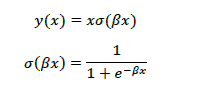
式を見ると分かるように、σ(βx)はシグモイド関数になっています。
β=1の場合のグラフを描いてみます。
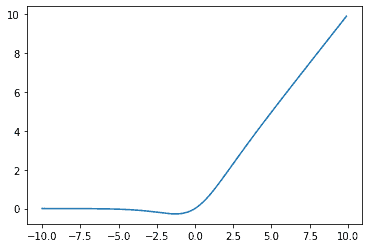
コードは以下のようになります。
import numpy as np
import matplotlib.pyplot as plt
def sigmoid_function(x):
return 1 / (1 + np.exp(-x))
def swish(x):
return x * sigmoid_function(x)
x = np.arange(-10.0, 10.0, 0.1)
y = swish(x)
plt.plot(x, y)
plt.show()
最近の活性化関数②Mish関数
Mish関数は、さらに最近の2019年に提案された活性化関数になります。
Swish関数よりも良い性能を発揮することが分かっています。
式は次のように表されます。
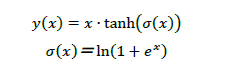
σ(x)はソフトプラス関数と呼ばれています。
グラフは以下のように表されます。
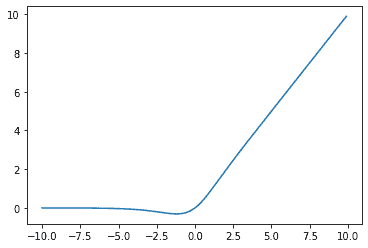
コードも載せておきます。
import numpy as np
import matplotlib.pyplot as plt
def softplus(x):
return np.log(1.0 + np.exp(x))
def tanh(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
def mish(x):
return x * tanh(softplus(x))
x = np.arange(-10.0, 10.0, 0.1)
y = mish(x)
plt.plot(x, y)
plt.show()
Swish関数とほとんど変わらないように見えますが、二つを重ねてみましょう。
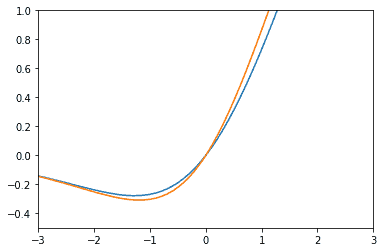
青線がSwish関数、オレンジ線がMish関数になります。
グラフより、x=0付近の変化がMish関数の方がダイナミックであることが分かります。
これは誤差が顕著に伝わることを示します。
ただ、指数計算が多いので、計算に少し時間がかかるといった点もあげられます。
Mish関数は、実装が簡単で効果も高いためニューラルネットワークにおいて最近注目されている活性化関数になります。
最後に
以上、ニューラルネットワークにおける代表的な活性化関数を紹介しました。
それぞれの関数によって、メリットデメリットがありますが、構築するモデルにあったものを用いて使いこなすことができると良いですね。
様々な活性化関数についての動画もこちらから見られます。
最後までご覧いただきありがとうございました。