今回はAIの回帰分析とはどんなものなのかや回帰分析でもっとも重要なデータの分析方法まで紹介していきます。
回帰分析について理解したい人や、やり方を知りたい人はぜひ参考にしてください。
回帰分析とは
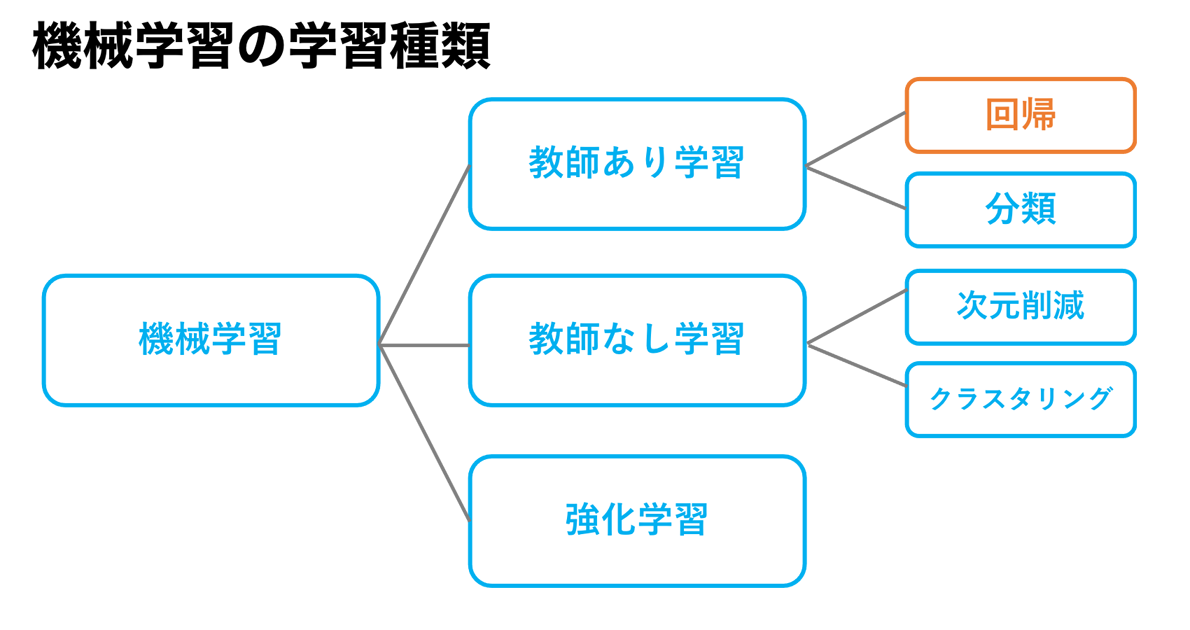
回帰分析とは過去のデータに基づいてある数値を予測することをいいます。
例えば「過去の競馬のデータから、今日のレースで勝つ馬を予想」したり、「過去の当たりデータからパチンコで当たりやすい席を予想」することができる機械学習の手法です。
データに基づかない予測はここでいう予測といいません。
回帰分析の簡単なアルゴリズム
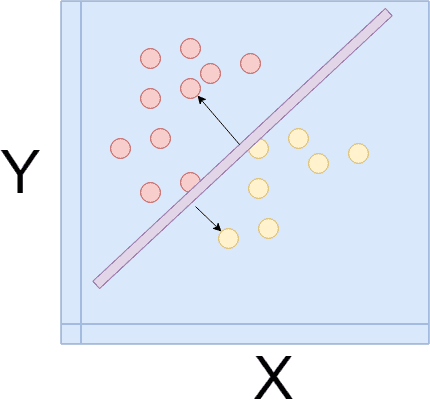
回帰分析における基本的なアルゴリズムである、線形回帰について説明をします。
平易的ではありますが、ある程度内部の中身を知っておいた方が、応用が効くのではないかと思います。
線形回帰(LinearRegression)は線形、つまり直線で分類可能なデータの境界線を学習によって見つけていく計算方法です。
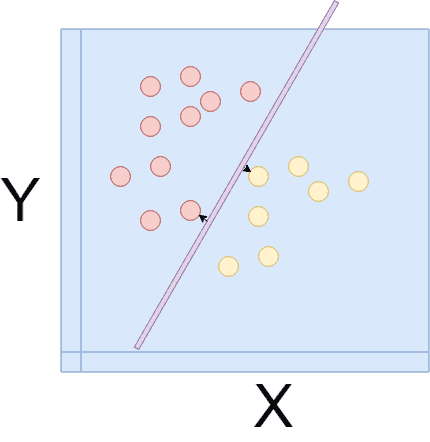
最初分類できる直線の辺りをつけてから、損失関数や最小勾配法などといった関数を使っていき一番最適な分類方法をとる直線式、Y=aX+bを求めていきます。
AIの回帰分析で必要なデータ
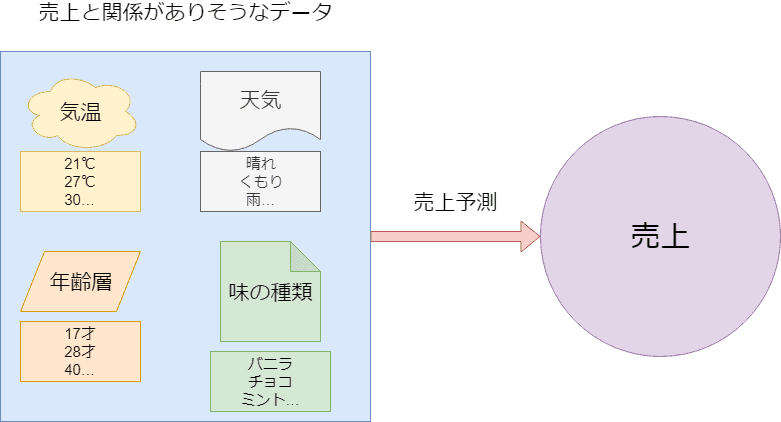
それではどういったデータが必要になってくるかというと、例えば予測したい数値が商品の売上であるなら、データはその商品の売上に「関係がありそうな」数値です。
商品がアイスクリームであれば、気温が高いのか低いのか、砂糖の量なのか、人の出入りの数なのかなど、何か売上に関係してそうな情報値のことを指します。
AIの回帰分析で使う専門用語
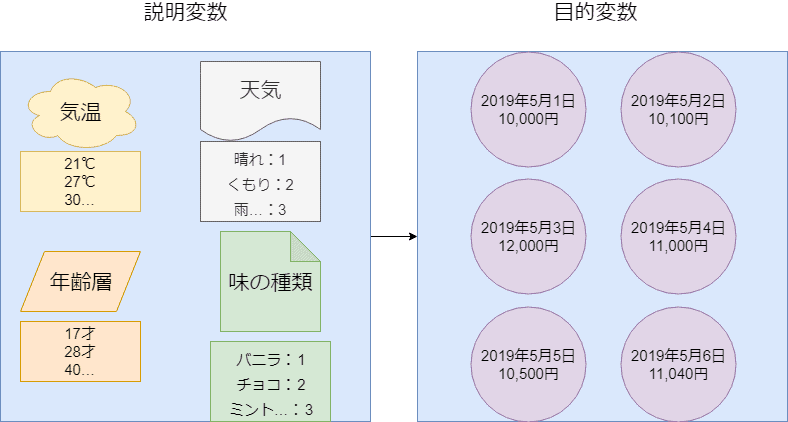
回帰分析において様々な専門用語を目にすることがあると思いますが、今必要なのは4つだけ、目的変数と説明変数、連続的数値と離散的数値です。
一つずつ簡単に説明していきます。
目的変数とは、予測したい値(明日の売上など)
そして説明変数とは、予測に使うデータの値をいいます。
連続的数値とは、17,000円、17,001円、17,002円のような字のごとく連続して並んでいる数値を言います。
気温などもそうで、21度の次が50度とはなりませんよね。
身長などもそうで、170mの次が180mとはなりません。
170.1mもあれば、170.0001mも存在します。
そして離散的数値というのは、サイコロの目や、電源のオンオフ、クリックをしたか、していないかなどです。
一般的に物事がはっきりと分けられていて、分類できる事象を数値化したものを指します。
YESかNOを数値化すると0か1、1か100にしても良いです。
大事なのは数値と数値の間の境目がはっきりとしていて、それによって、どっちがどの分野なのかが明確になっていることです。
そして、回帰分析によって予測する数値は売上の予想のような連続する数値、離散的ではない数値を分析することをいいます。
回帰分析を使ったAIのプログラミング方法が学べるおすすめのセミナーは!?
プログラミングを通してAIエンジニアの様々なことを学習できるおすすめのセミナーをご紹介します。
AI研究所が開催している、回帰分析を使ったAIのプログラミング方法が学べるAIエンジニア講習は、AIプログラミングを3ヶ月で習得できる、AIエンジニア育成セミナーです。
いつでもどこでも学習できるパソコン、スマホ、タブレット対応のeラーニング学習の為、自分の都合の良いペースで取り組めます。学習期間の目安は3ヶ月、全12回の講座を動画で視聴しながら自分のペースでしっかり学習できます.
内容は、実務で使えるAIの実装技術と活用術を習得できるおすすめのセミナーです!
「対面での受講の方が良い」、「直接講師に質問できる環境で学びたい」といった方は、3日間の学習コースが設けられていますのでご安心ください!
対面での学習を希望される方は会場受講を、遠方から参加したい方はライブウェビナーを検討してみてください。
もちろん非エンジニアの方でも、ゼロからプログラムの実装方法を学ぶことができます。
回帰分析のやり方
ある程度、回帰分析を使って未来の数値を予測するということがどういうことなのか見えてきたところで、実際の具体的な例を交えながら数値予想のモデルを作成していきましょう。
手を動かしながら実際の数値を見ていった方が、ただ受動的に理論を学ぶより遥かに理解が深まります。
Scikit-Learn
今回は簡単にインストールできて、すぐに機械学習などに必要なデータセット、アルゴリズムなどが利用できる便利なライブラリ、Scikit-Learnを使います。
Python環境が整っているなら、pipを使ってコマンドライン上一発でインストールできます。
回帰分析で住宅価格を予想してみた
それでは実際に回帰分析をしていきます。
使用するデータセットは、Scikit-Learn標準装備のBoston house prices dataset(ボストンの住宅価格)です。
ライブラリをインポート
必要なライブラリをインポートしていきます。
尚今回使用するエディターはJupyter Notebookです。
import matplotlib.pyplot as pltimport pandas as pd
import seaborn as sns%matplotlib inline
データセットをインポート
続いて、データセットをインポートしていきます。
boston_dataset = load_boston()
データセットの中身
まず、どんなデータセットにどんな値が入っているのかを見ていきます。
出力結果
| data | 様々な住宅の情報が入っている(説明変数) |
|---|---|
| target | 住宅価格(目的変数) |
| feature_names | 説明変数の列名 |
| DESCR | このデータセットの説明 |
pandasを使って、テーブル表記にし、何が入っているかを見やすくしましょう。
boston.head()
出力結果
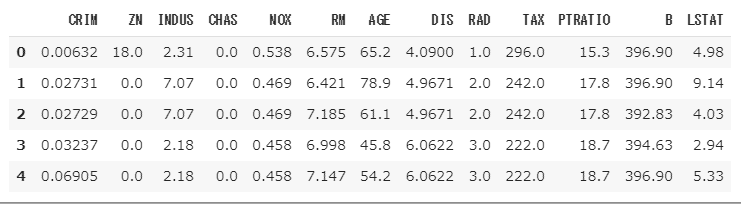
feature_namesに入っている列名の説明
| CRIM | 人口1人あたりの犯罪発生率 |
|---|---|
| ZN | 25,000平方フィート以上の住居区画の占める割合 |
| INDUS | 小売業以外の商業が占める面積の割合 |
| CHAS | チャールズ川によるダミー変数(1:川の周辺、0:それ以外) |
| NOX | NOXの濃度 –> NOXとは、排ガスや工場設備などから発生し,大気汚染の原因となる。 窒素酸化物の総称。 |
| RM | 住居の平均部屋数 |
| AGE | 1940年より前に建てられた物件の割合 |
| DIS | 5つのボストン市の雇用施設からの距離(重み付け済) |
| RAD | 環状高速道路へのアクセスしやすさ |
| TAX | $10,000 ドルあたりの不動産税率の総計 |
| PATRATIO | 町毎の児童と教師の比率 |
| B | 町毎の黒人 (Bk) の比率を次の式で表したもの。 1000(Bk – 0.63)^2 |
| LSTAT | 給与の低い職業に従事する人口の割合 (%) |
回帰分析で重要なデータの設定
上のリストにて、2点、回帰分析において重要な元データの設定用語がでてきたので説明します。
ダミー変数
ダミー変数とはカテゴリー型のデータを0か1で表現し直す変数のことです。
上の例でいうと、CHAS列にはチャールズ川の周辺か、それ以外というカテゴリー分けがなされています。
そして、チャールズ川の周辺であれば1にして、それ以外は0という「数値」に直します。
例えば曜日をダミー変数にする場合。
月曜日から日曜日までを0から6にして、そこから列名として月曜日から日曜日に直し、月曜日であれば1、そうでないなら0にします。
同様に火曜日であれば1、と順次直していきます。
曜日番号
| 月曜日 | 0 |
|---|---|
| 火曜日 | 1 |
| 水曜日 | 2 |
| 木曜日 | 3 |
| 金曜日 | 4 |
| 土曜日 | 5 |
| 日曜日 | 6 |
さらに変換する
インデックス番号月曜日火曜日水曜日木曜日金曜日土曜日日曜日
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
重み付け
続いては重み付けです。
「重み」を簡単に説明すると貢献度、信頼度、評価の度合いです。
このデータセットで「重み」がつけられているのは「距離」です。
距離には様々な測定法があり、地形、勾配などが考慮されます。
その考慮された中に「信頼性」の高い測定方法、測定基準が存在します。
その「信頼度」こそが「重み」あり、一つの距離測定に対して、「重み」が違う値同士を
その測定の重みを考慮した加重平均で計算し、最確値として導き出した値が、いわゆる「重み付けされた値」です。
目的変数を取り出す
続いては予測したい住宅価格をデータセットから取り出し、データフレームに加えます。
回帰分析で重要なデータの前処理
続いて欠損値です。
欠損値とは何らかの理由で、データが取れなかった値などを指し、これが入っていると学習精度が下がります。
これらを取り除いていく作業も重要です。
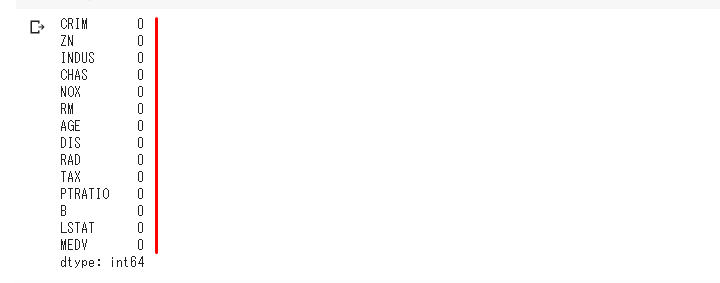
幸いに、今回のデータセットでは欠損値はないようです。
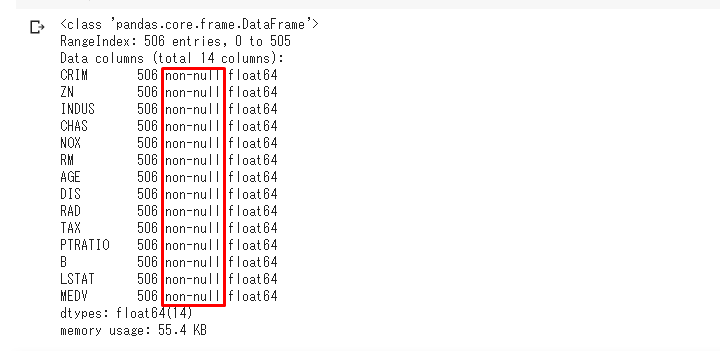
欠損値を探す他のやり方としては、info()メソッドを使うなどがあります。
実行すると下の画像の赤枠部分に情報がでます。
回帰分析を使ったAIのプログラミング方法が学べるAIエンジニア育成講座はこちら
回帰分析でもっとも重要な元データの分析
続いて、回帰分析において、もっとも重要であるデータの分析をおこなっていきます。
ここでは、目的変数と他の特徴とで、どんな関係性があるのかをいくつかグラフにして、確認していきます。
まずは目的変数をグラフにしてみます。
sns.set(rc={‘figure.figsize’:(12,9)})
# ヒストグラムを表示させます。binsはX軸のメモリの細かさです。
plt.show()
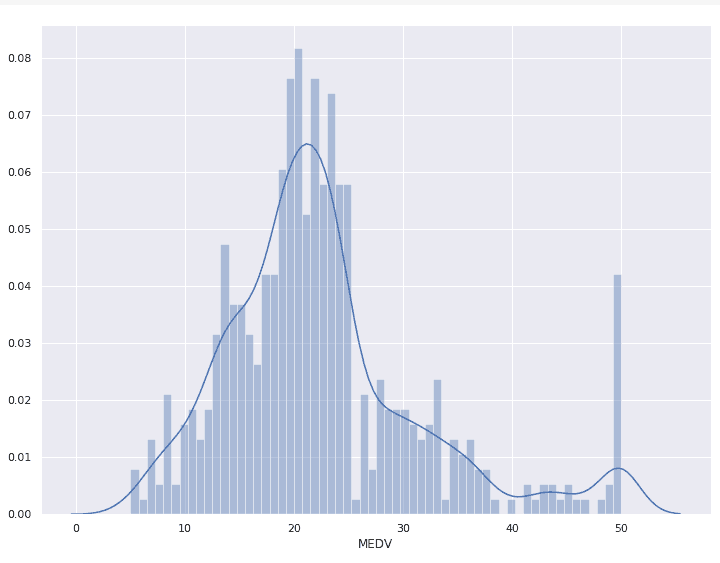
ほんの少しバラけていますが、正常に分布しているようです。
続いて、PandasのCorrメソッドで相関行列を作り、
それをヒートマップにして、2つの値の相関関係を調べていきます。
correlation_matrix = boston.corr().round(2)
# annotをTrueにすると数値をグラフ内に表示してくれます。
sns.heatmap(data=correlation_matrix, annot=True)
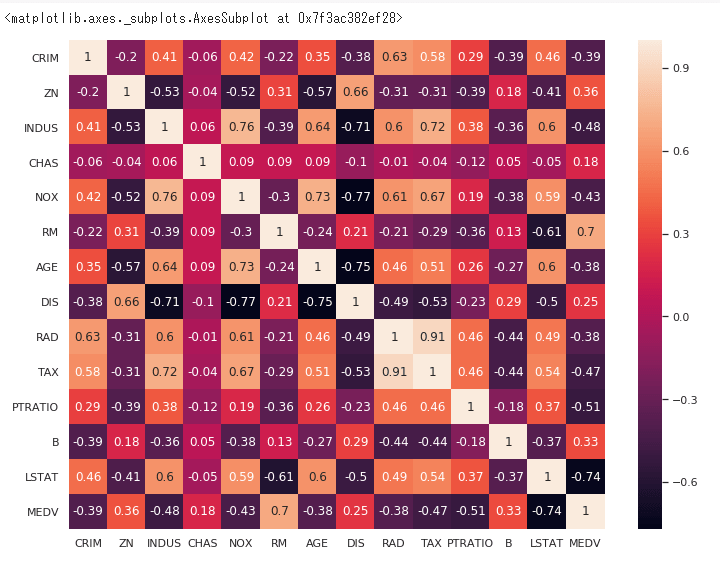
この図にある一つ一つの値は1から−1までの幅があり、
1に近いほど、強い正の相関があり、−1に近いほど、強い負の相関があります。
データの特徴選択
回帰モデルの学習の精度をあげるために特徴選択に挑戦しましょう。
まずは目的変数(MEDV)と高い相関性をもつ特徴を探しましょう。
さっと見渡してみるとRMはMEDVと強い正の相関性(0.7)をもっています。
そしてLSTATはMEDVと強い負の相関性(-0.74)をもってるといえます。
特徴選択の注意事項
もう一つ、特徴選択で気をつける事はマルチコ(多重共線性)を確認することです。
マルチコ(多重共線性)とは、とどのつまり、お互い強い相関関係をもった説明変数同士のことです。
こういった説明変数同士を一緒にしてしまうと、正しく回帰モデルの学習ができなくなってしまうため、
これらをすべて学習モデルに入れてはいけません。
それを踏まえた上でもう一度ヒートマップをみてみると、
RADとTAXは0.91ポイント。この2つは互いに強い相関性があります。
そして、DISとAGEも同じように相関性が近いのでどちらか一つを省く必要があります。
散布図にトライ
特徴選択の内容がなんとなく掴めたと思います。
そこで、散布図を使って相関関係というものがどうような状態か目で見て確認しておきましょう。
それでは目的変数(MEDV)と強い相関を示した、RMとLSTATの特徴がどうような関連性をもっているかグラフで見てみましょう。
plt.figure(figsize=(20, 5))# 2つの特徴に1つの目的変数をつかう。
features = [‘LSTAT’, ‘RM’]target = boston[‘MEDV’]# 2つのグラフを1ページで表示するため
#For文を使い、一つずつグラフ作っていく。
for i, col in enumerate(features):
plt.subplot(1, len(features) , i+1)
x = boston[col]y = target
plt.scatter(x, y, marker=’o’)
plt.title(col)
plt.xlabel(col)
plt.ylabel(‘MEDV’)
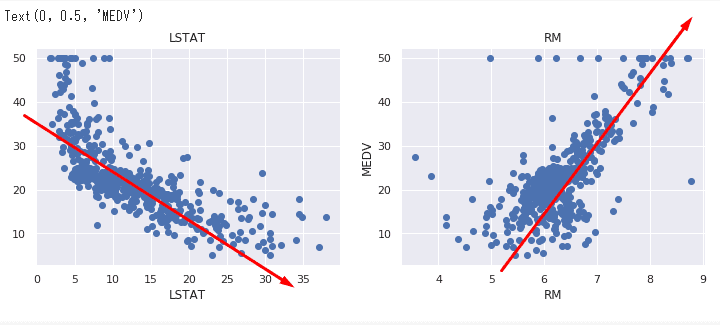
相関関係の説明
左側はLSTAT、給与が低い人たちの割合が高くなるほど、負の相関になる。
つまり住宅価格は下がっている。
逆に右側、RM、部屋の数が多いほど、正の相関になる。
つまり住宅価格は上がっている。
住宅価格予想
いよいよ回帰モデルを機械に学習させて住宅価格を予測させていきます。
学習に邪魔なノイズ的な特徴を排除して、強い相関性をもつLSTATとRMのみを使って学習モデルを作ります。
# 新たに列名を指定して、Xつまり説明変数とします。
X = pd.DataFrame(np.c_[boston[‘LSTAT’], boston[‘RM’]], columns = [‘LSTAT’,’RM’])
# もちろんY、目的変数には住宅価格を入れます。
Y = boston[‘MEDV’]
過学習を避ける
ここで回帰分析においてもう一つ気をつけなければならない厄介者がいます。
それは過学習(Overfitting)と言って、手元にあるデータ全てを使ってしまい、未知のデータに対応できなくなってしまった学習モデルを指します。
その過学習を避けるために、もっとも手っ取り早いのが学習データを8対2程度の割合で分けて、
学習用と検証用にして、先に学習用で学習を行い、検証用を擬似的に未知のデータとして使用して様子を見て、精度を確認する方法です。
そのためにScikit-Learnに用意されている便利な関数、train_test_splitを使います。
from sklearn.model_selection import train_test_split# テストサイズを2割にして、Random Stateは5
# つまり、乱数の種に5を指定して、乱数を生成させるという意味。
# 疑似乱数を固定することにより、ランダムではあるが、再現性があるため
# 機械学習におけるランダム設定には欠かせない。
# なぜなら、学習結果がランダムにしたから変わったのか、判別がつかなければ、
# 学習の検証にならないから。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state=5)
print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)
出力結果
(102, 2)
(404,)
(102,)
学習と検証
さあ、いよいよ大詰めです。Scikit-Learnの回帰アルゴリズム
LinearRegressionを使って学習用と検証用の回帰モデルを作っていきましょう。
from sklearn.linear_model import LinearRegression
# 学習用モデルの箱を作ります。
lin_model = LinearRegression()
# トレーニング開始です。
lin_model.fit(X_train, Y_train)
学習モデルの評価
学習が終わったら、きちんと精度がでているかを、
2つの回帰分析の精度評価指標を使って調べてみましょう。
from sklearn.metrics import mean_squared_error
# R2 (決定係数) の計算関数
from sklearn.metrics import r2_score# 学習用の目的変数の予測値を出す。
y_train_predict = lin_model.predict(X_train)# Root Mean Squared Error (RMSE) 関数でRMSEの値を算出。
rmse = (np.sqrt(mean_squared_error(Y_train, y_train_predict)))
# R2 関数でR2の値を算出。
r2 = r2_score(Y_train, y_train_predict)print(“学習用モデル成果”) print(“————————————–“)
print(‘RMSE の値は {}’.format(rmse))
print(‘R2 スコアは {}’.format(r2))
print(“\n”)# 検証用のモデルと評価値を作成。
y_test_predict = lin_model.predict(X_test)
rmse = (np.sqrt(mean_squared_error(Y_test, y_test_predict)))
r2 = r2_score(Y_test, y_test_predict)print(“検証用モデル成果”)
print(“————————————–“)
print(‘RMSE の値は {}’.format(rmse))
print(‘R2 スコアは {}’.format(r2))

Root Mean Squared Error (RMSE)
2つの回帰分析の精度評価指標のうち1つ目です。
こちらは平均化された誤差の値を表します。
0に近いほど予測精度が高いことを表します。
R2 (決定係数)
R2 (決定係数)は1に近いほど精度の高いことを表します。
学習用と検証用とでは、さほど数値の開きは見られませんでしたが、
どうやら精度があまり良くないみたいです。特にRMSEの値が悪いです。
これらを改善するには、特徴量を増やしたり、アルゴリズムを変えるなどといった工夫が必要です。
(今回は、全体の流れを理解していただくため、改善の作業は行いませんでした)
終わりに
最後に、実際にこの学習済みモデルによって予測した数値を確認します。
実は上のコードで既に求めていたので、後はそれを見るだけです。
y_train_predict = lin_model.predict(X_train)print(“学習用モデル成果”) print(“————————————–“)
print(‘学習用モデル予測値の数値 {}’.format(y_train_predict))
print(“\n”)# 検証用の目的変数の予測値。
y_test_predict = lin_model.predict(X_test)print(“検証用モデル成果”)
print(“————————————–“)
print(‘学習用モデル予測値の数値 {}’.format(y_test_predict))
print(“\n”)
学習に使用したデータを、学習済みモデルに予測させた出力数値
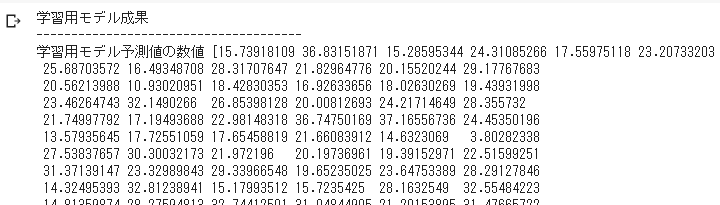
検証用に取っておいたデータを、学習済みモデルに予測させた出力数値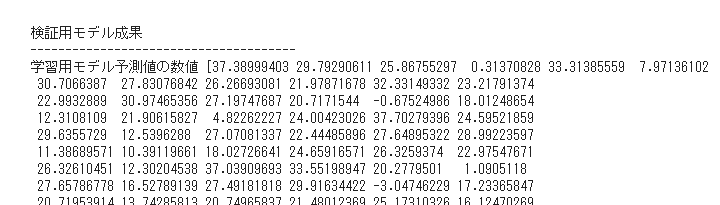
このままでは分かりづらいので、グラフ化して比較してみます。
# 分かりにくいのでグラフ比較
print(“学習用モデル成果”)
print(“————————————–“)
# figuresizeは描写するグラフの画面サイズです。
sns.set(rc={‘figure.figsize’:(12,9)})
# ヒストグラムを表示させます。binsはX軸のメモリの細かさです。
sns.distplot(y_train_predict, bins=60)
plt.show()
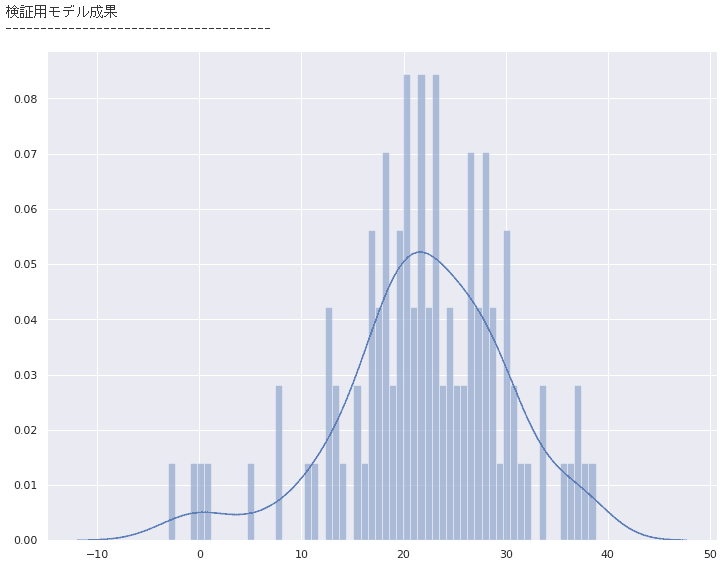
print(“検証用モデル成果”)
print(“————————————–“)
sns.set(rc={‘figure.figsize’:(12,9)})
sns.distplot(y_test_predict, bins=60)
plt.show()
# 元のデータ
print(“本来のデータ”)
print(“————————————–“)
sns.set(rc={‘figure.figsize’:(12,9)})
sns.distplot(boston[‘MEDV’], bins=60)
plt.show()
学習に使用したデータを、学習済みモデルに予測させた出力数値のグラフ
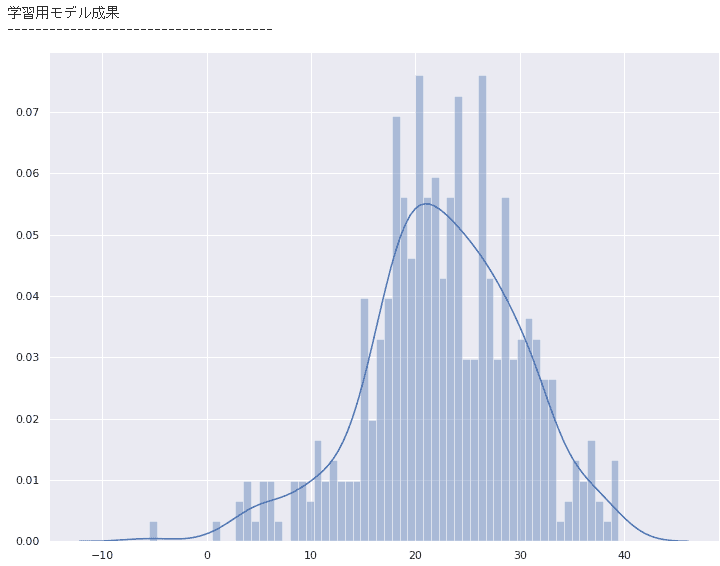
検証用に取っておいたデータを、学習済みモデルに予測させた出力数値のグラフ
元のデータのグラフ
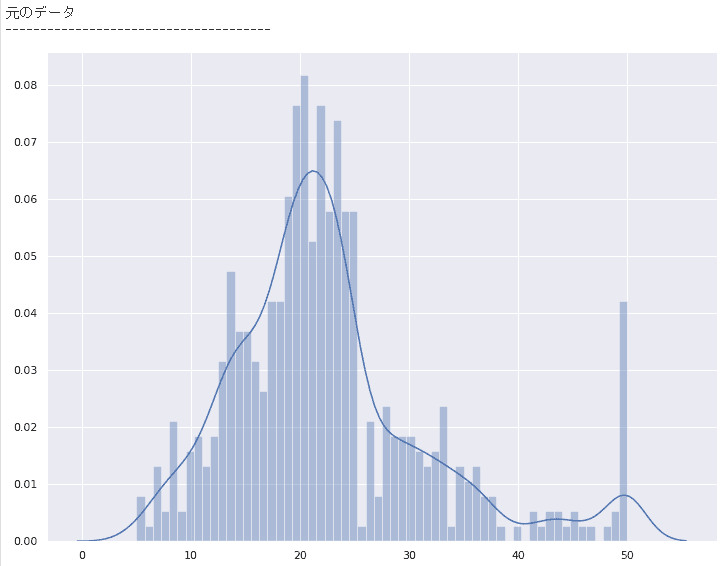
精度が良いモデルができていると、元のデータのグラフと近いグラフの形が予測結果のグラフとして表示されますが、あまり上手くいっていないことが分かります。
特徴量を増やす、データ集約をするといったデータの前処理と、線形回帰以外の機械学習アルゴリズムを利用するなどの2つの側面から試行錯誤をしていく必要があります。
AIが学べるおすすめのセミナーの紹介!
今回紹介した回帰分析を使ったデータ分析は、初心者にとってはハードルが高いことも多いですよね。
初心者から成りあがるにはセミナーが一番手っ取り早いです。
先程も記事内でご紹介しました、AI研究所主催のイチオシのAI講座は…
- ノーコードでAIを作る講座を短期間で受けたい場合 → ビジネス向けAI講習
- AIプログラミングを3ヶ月でしっかりと習得したい場合 → AIエンジニア講習
こちらの2つが主におすすめのAI講座になっています!
「ビジネス向けAI講習」は、AIの仕組みや作り方、ビジネスでAIを活用する方法を1日で学ぶことができるセミナーです。
プログラムコードを使わずにAIを作りながら学ぶことができるため、AIプロジェクトのマネージャーなどにおすすめのセミナーです!
また、「AIエンジニア講習」は、AIプログラミングを3ヶ月で習得できる、AIエンジニア育成セミナーです。
いつでもどこでも学習できるパソコン、スマホ、タブレット対応のeラーニング学習となっており、学習期間の目安は3ヶ月、全12回の講座を動画で視聴しながら自分のペースでしっかり学習できます。
プログラミング手法、基礎AIの実装から応用AIの実装までを学び、ライブラリの使い方も学べるのでAIモデルが使えるようになります。
最終的には、高度なデータ処理も学ぶことでAIプログラミングマスターを目指すカリキュラムです。
「ビジネス向けAI講習」や、「AIエンジニア講習」に参加すれば、AI理論やPythonプログラミングの基礎から、ライブラリを使用したディープラーニングの実装など、実務に繋がる分野まで学ぶことができます。
どちらのセミナーも初心者向けで、AIが全く分からなくても受けられる講座とのことなので安心です。
さらに、JDLA認定のE資格対策講座を受けたい場合、AI研究所が開催している「E資格講習」という、最短でE資格の合格を目指すセミナーもございます。
E資格試験の受験資格を得るためには、日本ディープラーニング協会(JDLA)が認定したプログラムの受講修了が必須となります。
日本ディープラーニング協会にて規定されている出題範囲をすべてカバーしているセミナーなので、常に最新のE資格に完全対応しており、試験対策を中心に、E資格に合格するためのポイントを絞って学習できます。
本講座を修了することで、E資格の受験資格を短期間で確実に取得することができます。
この機会にセミナーを受講してみてはいかがでしょうか?
席数に限りがございますのでお早めにお申し込みくださいね!
AIの回帰分析についてまとめ
今回はAIの回帰分析がどんなものかや、実際に回帰分析のやり方や手順を説明しました。
回帰分析と聞くと一見難しそうですが、機械学習の中でも基本的な手順で行うことが可能です。
ぜひこの機会にAIの回帰分析で、過去のデータから自動で分析してみてください。