教師あり学習はどのような仕組みなのか、よくわからない人も多いと思います。
今回は教師あり学習はどのようなアルゴリズムになっているのかや、4種類のアルゴリズム別に特徴ややり方を解説していきます。
教師あり学習とは?
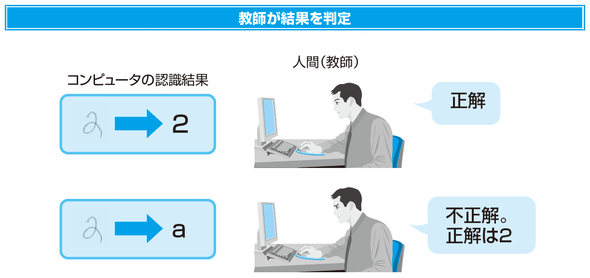 出典:https://image.itmedia.co.jp/ait/articles/1610/01/r20_img02_04.png
出典:https://image.itmedia.co.jp/ait/articles/1610/01/r20_img02_04.png
さて、そもそも教師あり学習とは一体どのような学習のことだったでしょうか。
教師ありと言うくらいなので、そのまま教師がいる学習と読み替えても問題はなさそうです。
ここでは、機械に学習させる過程を想定した機械学習でもある教師あり学習とは何か?を見ていくことにします。
まず、機械に学習させていく際に、必要なデータが必要なのですが、それは教師データと言われるものになります。
この教師データとは、正解のラベル付けをされたデータのことを指します。
例えば、数字の画像とその数字が1なのか3なのかといったデータセットのことです。
つまり、あるデータ+そのデータの正解ラベルを合わせたデータセットのことを教師データと言います。
この教師データを使うことにより、未知のデータに対しての予測していくことが可能になります。
上記のように、コンピュータが認識した結果(出力値)と教師が示した値(正解値)を組み合わせながら、学習を進めていきます。
なるべく正確な予測がつくように、出力値と正解値の誤差を小さくしていくことで学習器の精度向上に繋げていきます。
教師あり学習についての理解をより深めたい場合は、下記記事を参考にしてください。
それでは、ここまで教師あり学習の概要を見てきたので、具体的なアーキテクチャを元に教師あり学習の理解を深めていきましょう。
教師あり学習の種類とは
今回は、機械学習の一つである教師あり学習の中から代表的な4つのアルゴリズムの特徴を紹介していきます。
- ロジスティック回帰
- SVM(サポートベクターマシン)
- k近傍法
- 決定木
の以上4つのアルゴリズムです。
この4つのアルゴリズムについて詳しく解説していきます。
1.ロジスティック回帰
まず最初にご紹介するのが、ロジスティック回帰(logistic regression)です。
このロジスティック回帰(logistic regression)とは、単純パーセプトロンの活性化関数にシグモイド関数を使用したモデルです。
回帰という名前がついているため、回帰問題と思われますが分類問題に使用していきます。
出力層にシグモイド関数を使用することで、目的変数を0~1の数値に変換されるため、それを確率の値として2値のクラス分類ができます。
また、複数の分類を行いたい場合には、出力層にソフトマック関数を使用することで多クラス分類をすることが可能です。
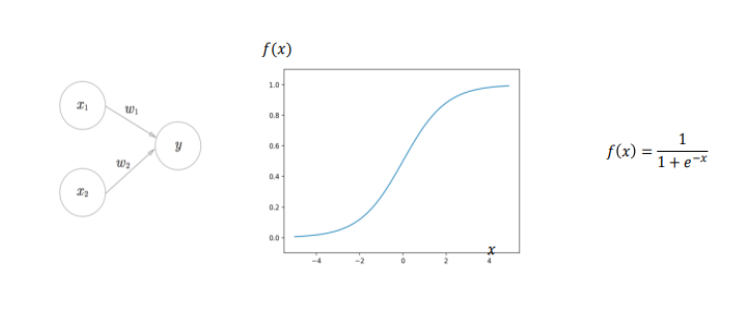
シグモイド関数に当てはめると…
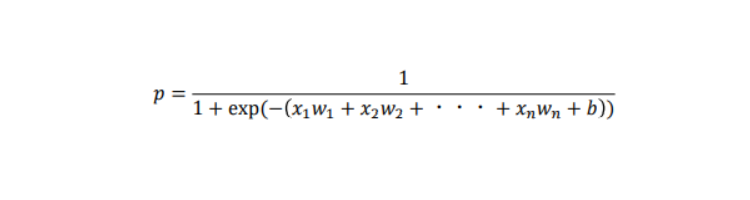
上記でも触れましたが、このロジスティック回帰では、求める目的関数は確率(0~1)になります。
ある事象が起こる確率を起こらない確率1 − で割ったものをオッズと呼び、オッズの対数を取ったものをロジットと呼びます。
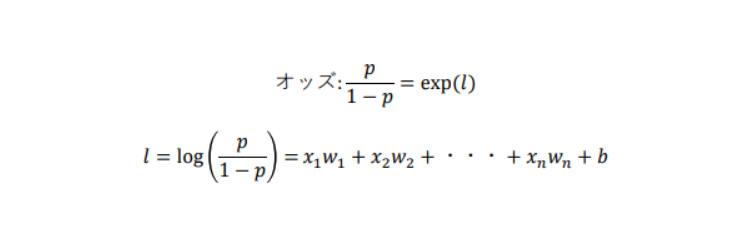
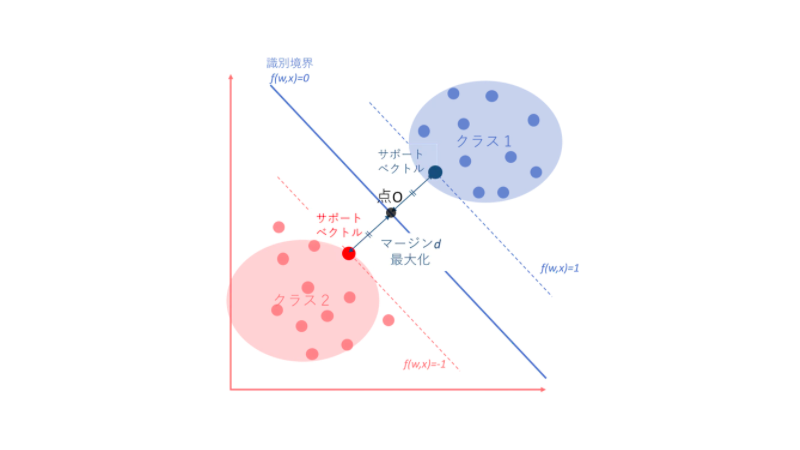
2.SVM(サポートベクターマシン)
続いて、教師あり学習の二つ目であるSVM(Support Vector Machine)を見ていきましょう。
SVMはパーセプトロンに
- カーネル関数
- マージン最大化
を加えて次元を増やすことで、非線形の分割を線形に分割できるようにしています。
クラス分類と回帰が扱えるアルゴリズムです。
ここまでの説明では一見簡単そうに思えますが、この二つを求めるのにあらゆる数式を経ながら求めなくてはなりません。
より深めたい方のために、下記に計算過程を記載しているので、是非参考にしてみてください。
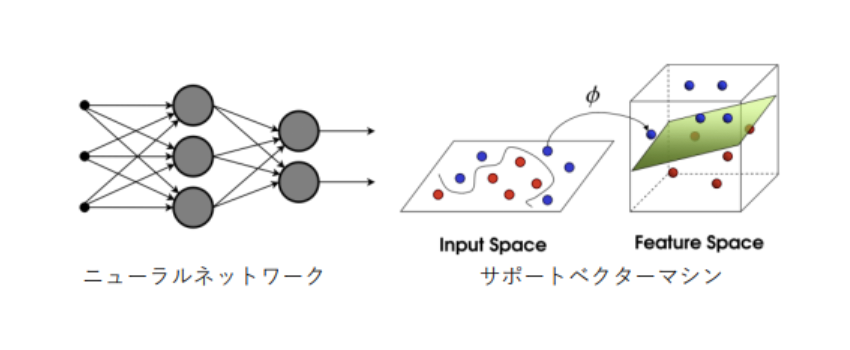 出典:https://ja.wikipedia.org/wikiニューラルネットワーク
出典:https://ja.wikipedia.org/wikiニューラルネットワーク
出典:http://i.imgur.com/
カーネル関数
カーネル関数とは、非線形の特徴量をデータ表現に加えることで次元を増やし、分離をする際に使用 されるアルゴリズムです。
実際にデータポイントの拡張を計算すると高次元で計算量 が多くなりすぎるため、数学的に式変形をして解決するカーネルトリックという手法が用いられる事が多くなります。
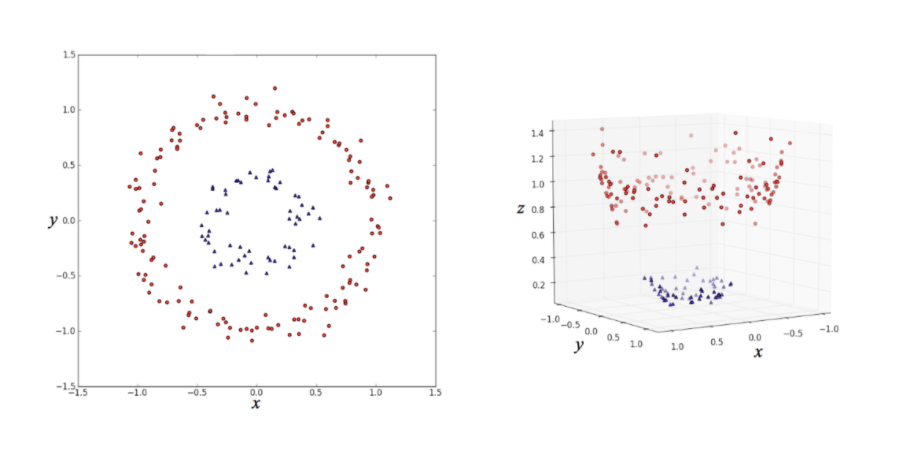 出典:https://cdn-ak.f.st-hatena.com/images/fotolife/e/enakai00/20171013/20171013103327.png
出典:https://cdn-ak.f.st-hatena.com/images/fotolife/e/enakai00/20171013/20171013103327.png
元々の特徴空間上の2点x, x′の距離に基づいて定義されるある関数κ(x, x′)を考える。
非線形写像をφ(入力xを高次元空間に写像する関数)とした時に、次の式が成り立つと仮定する:
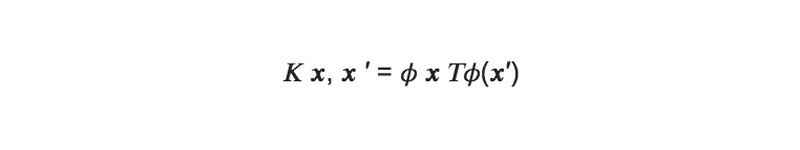
式の意味としては、元々の特徴空間での2点の距離が、ある非線形写像後の特徴空間での内積になり、2点間の近さの情報が保存されるとする。
この時、写像後の特徴空間での識別関数gは以下のようにあらわす事が出来る(g = 0:識別面):
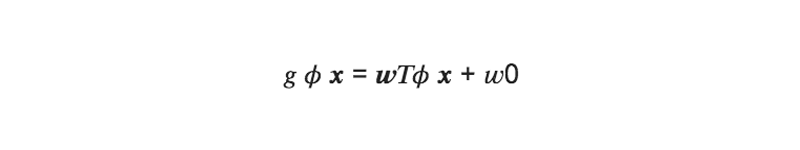
これらにSVMを適用すると
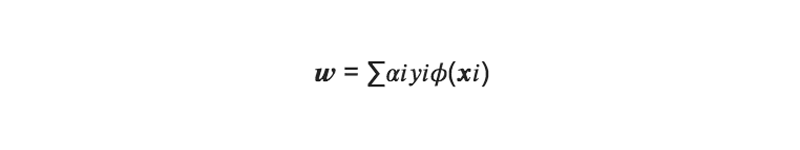
となるので、識別関数は次のようになる:
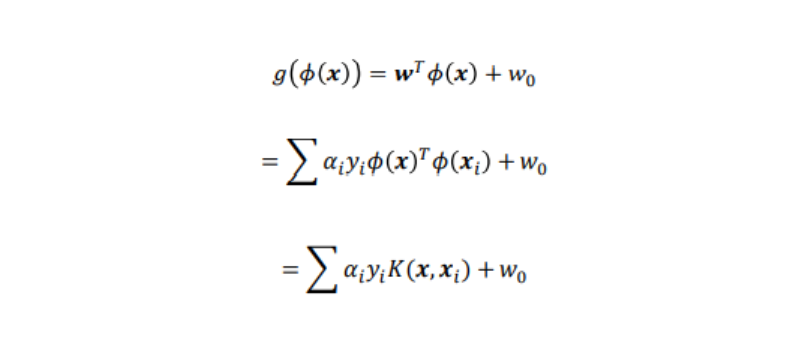
また、ラグランジュ関数については下記のようになる:
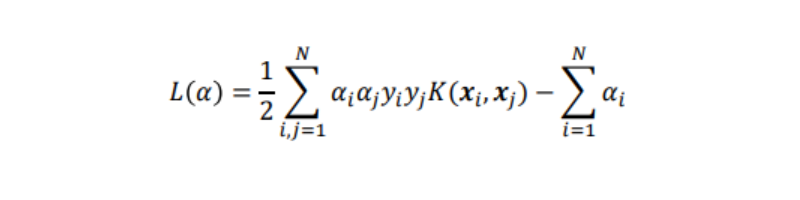
これらの結果から、識別関数にもラグランジュ関数についても、非線形写像φが存在しない式になっている。
このように直接非線形写像φを求める作業を避ける方法をカーネルトリックと呼んでいる。
カーネル関数には次のようなものがあります。

マージン最大化
「マージン最大化」とは、 マージンを最大にする位置を見つけることで汎化性能の高いモデルとするための考え方です。
マージンとは、分離する識別境界からいくつかの点に至る距離の最小値を言い、この境界から最も近いデータポイントをサポートベクトルと呼びます。
マージン最大化
教師あり/二値分類と仮定: xi , yi (i = 1,2, … , Ν), yi = 1 or −1 とすると、yが教師データで、1または-1を識別する問題と考える事が出来る。
このとき、識別面は次式で表される:
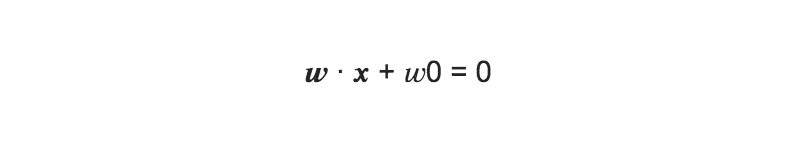
(yi = 1の時は、 w ∙ x + w0 > 0、 yi = −1の時は、 w ∙ x + w0 < 0)
この識別面を求める事が目的となる(wを求める)。→正負で二値分類の判定を行う
※w0 = −w ∙ x は、wが求まれば求まる。
xiと識別面との距離Dist(xi)は、点と距離の公式から次の式で表される(空間距離):
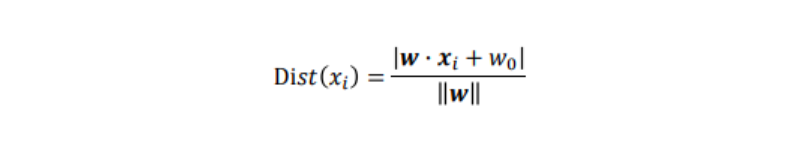
この時、学習データxiと識別面との最小距離は以下のようになる:
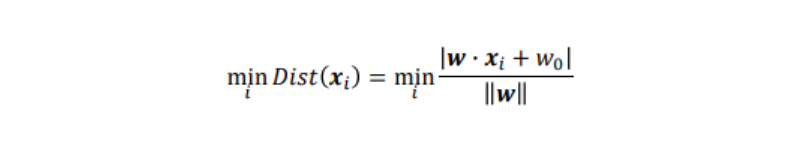
ここで識別面との距離が最も距離の近いデータを、識別面の左辺に代入した時に、その絶対値が1になるように、重みwを調整したと仮定する。
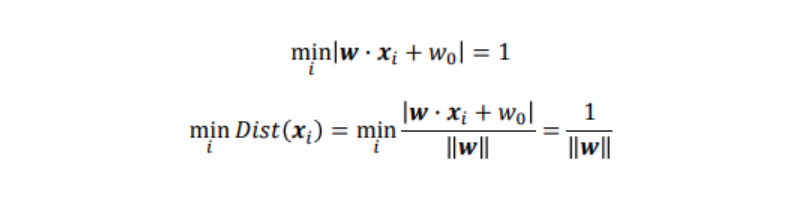
上式より、マージンを最大にする識別面を求める事は、1w を最大化、つまり、w を最小化する事に帰着される。
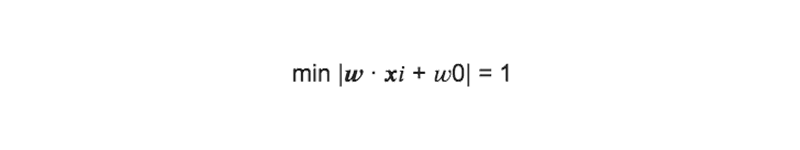
なので、次式が成り立つ:
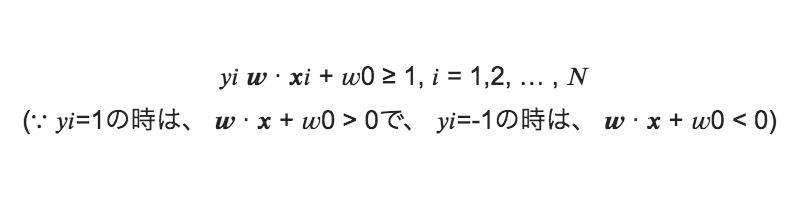
この条件の下、w の最小化を考える。
w のままだと計算上扱いづらいので、12 w 2を最小化する(12は後で微分を行うため)。
整理すると下記になる:
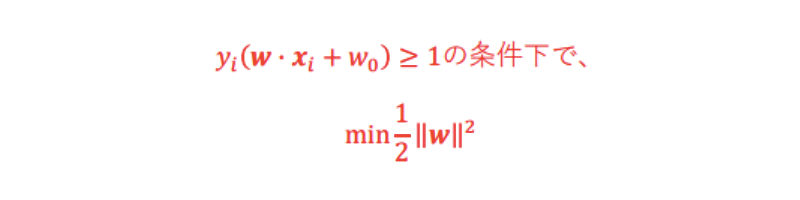
ここから「ラグランジュの未定乗数法」を用いて解を求める事を考える。
ラグランジュの未定乗数法とは、ある条件のもとで問題を普通の極値問題として最適化を行う方法です。
ラグランジュの未定乗数法
gx = 0(または gx > 0などの不等式)の条件下で、 fx の最小値を求める場合に利用。
ラグランジュ関数
L xλ, = fx + λgx (λ:ラグランジュ乗数)
として、この関数が極値xαを与えるのであれば、極値xαは L/x = 0 を満たす。
今回は、

と、おけるので、ラグランジュの未定乗数法を用いて、ラグランジュ乗数をαiとするとラグランジュ関数Lは、
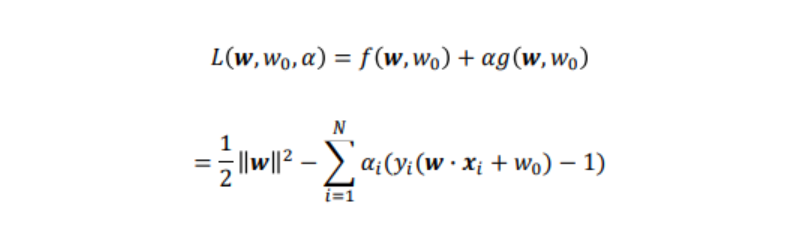
と書ける。
このラグランジュ関数をw, w0で偏微分した値はゼロなので、下記の式が成り立つ。

→ wを求めるためには、αを求めればよいということがわかった。
この2式をLに代入する:
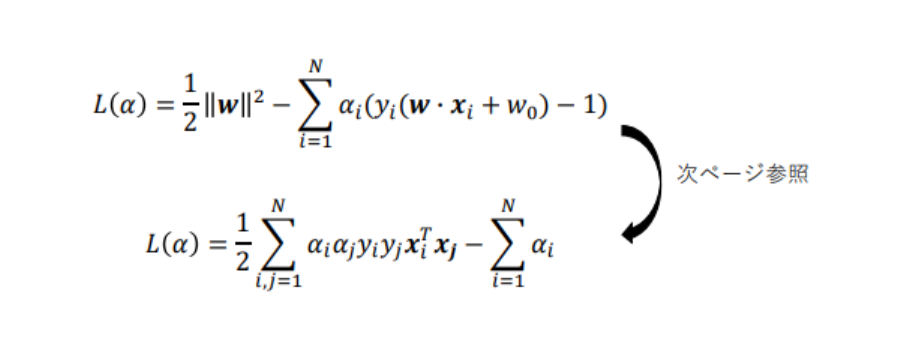
この上式を最小化するαiを求める事で、wとw0が求められる
(αiの二次計画問題として解く→2次関数の最小化→凸最適化→局所解がない)。

αiの二次計画問題を解くと、殆どのαiはゼロになる:
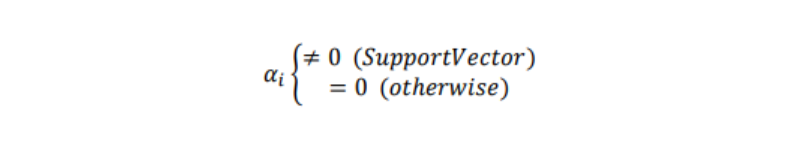
求めたαiからwを得る事が出来る(Lを偏微分した式を使う):
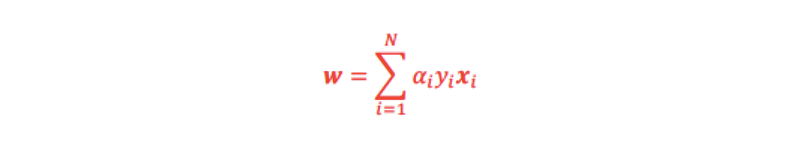
w0は、次式で求める事が出来る:

SVMに関しては下記記事でも解説しています。
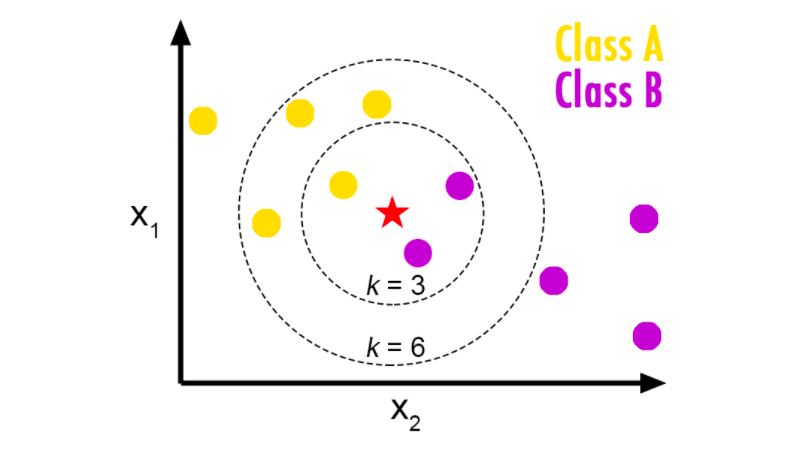
3.k近傍法
続いて、教師あり学習の三つ目であるk近傍法(k-NN:k-nearest neighbor algorithm)についてご紹介していきます。
このk近傍法(k-NN)は、クラス分類問題を解くことができるアルゴリズムです。
教師データからモデルのパラメータを推測することはせず、学習データをベクトル空間上にプロットしておき、未知のデータが得られたら、そこから距離が近い順に任意のk個を取得し、多数決でデータが属するクラスを推定していきます。
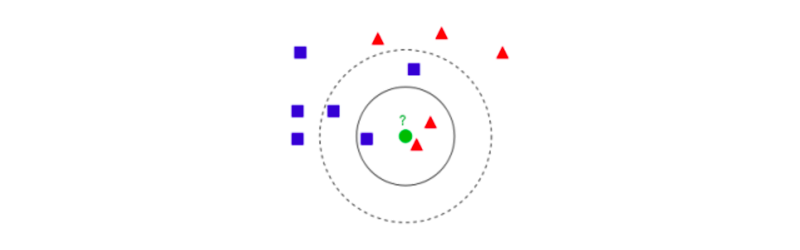
出典: https://ja.wikipedia.org/wiki/K%E8%BF%91%E5%82%8D%E6%B3%95
k近傍法でどのようにクラスを推定していくのかというと、まず、 既知のデータ(学習データ)をプロットしていきます。
その次に、任意でkの数を決めてから、未知のデータに対して近い点からk個のデータを取得します。
下図で見ると、kの数を3にした時(k=3)と、6にした時(k=6)とでは、選ばれるデータ数が違っているのを確認出来るかと思います。
ここで近い点を選ぶ際に使用するのが、ユーグリッド距離で、これは空間内の2点間をつなぐ線分の距離になります。
最後に、そのk個のデータのクラスの多数決で、属するクラスを推定します。
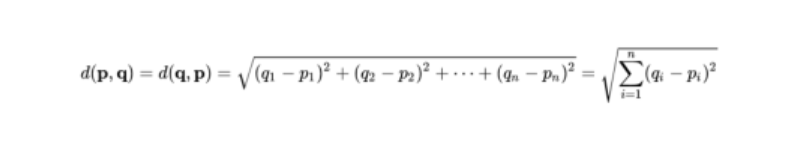
 出典:https://qiita.com/yshi12/items/26771139672d40a0be32
出典:https://qiita.com/yshi12/items/26771139672d40a0be32
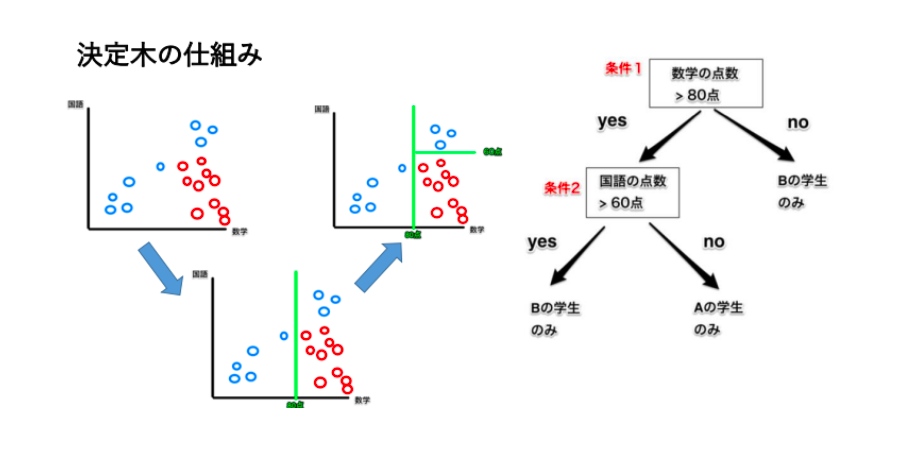
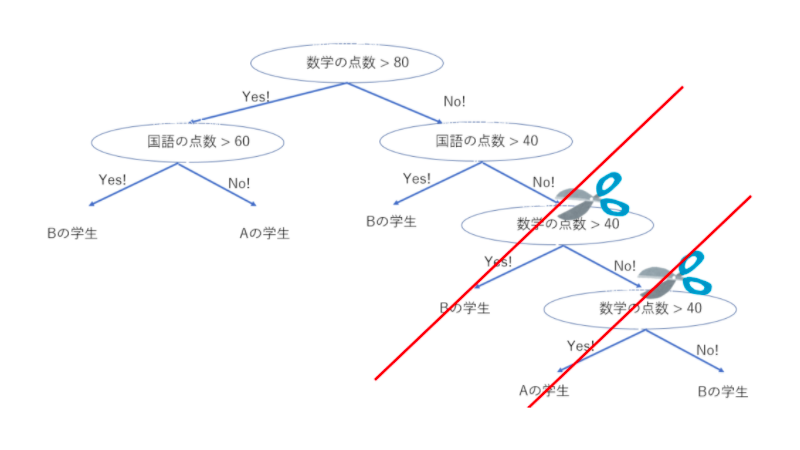
4.決定木
 出典:http://www.randpy.tokyo/entry/decision_tree_theory
出典:http://www.randpy.tokyo/entry/decision_tree_theory
最後にクラス分類と回帰ができる決定木というモデルを見ていきましょう。
この決定木は、Yes/Noで答えられる質問で構成された階層的な木構造を学習するアルゴリズムです。
条件分岐によってグループを分割して分類する手法で、代表的なものでは、CARTやC4.5(C5.0)がよく使用されています。
グループを分割する際には、グループがなるべく同じような属性で構成されるように分割していきます。
条件分岐が複雑になってくると過学習を起こしやすく、それに対応したのが後述する剪定(枝刈り)によってある程度は改善されました。
学習結果が把握しやすいため活用ケースが多く見られるアーキテクチャとなります。
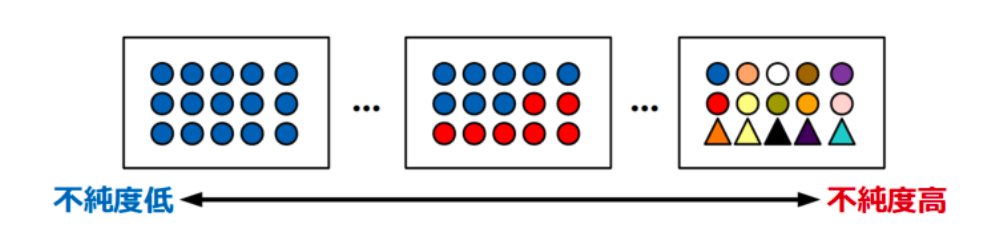
不純度
 出典:https://watlab-blog.com/2020/01/02/decision-tree/
出典:https://watlab-blog.com/2020/01/02/decision-tree/
決定木分岐では、不純度が0、つまりさまざまなクラスが混ざりあっていないデータセットの状態になるまで分岐させていきます。
1つの対象値のデータポイントしか含まないような決定木の葉(ノード)を純粋な葉と呼びます。
色々なクラスが混在するグループは不純度が高く、1つのクラスもしくは1つのク ラスの割合が大多数を占めるほど不純度は低くなります。
決定木では、分割後のグループの不純度が一番小さくなるような基準を選んで分割していくというのが基本的な流れです。
剪定
 出典:https://www.randpy.tokyo/entry/decision_tree_theory_pruning</a >
出典:https://www.randpy.tokyo/entry/decision_tree_theory_pruning</a >
決定木の概要で、過学習を起こしやすいというのがありました。
条件分岐が多くなるにつれて生じるこの過学習に対応したのが剪定(枝刈り)です。
葉が純粋になるまで分割を続けて木が大きくなればなるほど、厳密に分割できるようになる反面、汎用性が無くなってしまうというデメリットがあります。
そのため、木の深さを制限したり、葉の最大値を制限する剪定を行うことで汎化性能を高めます。
教師あり学習のアルゴリズムのメリット・デメリット
教師あり学習のアルゴリズムを紹介していきましたが、種類によってそれぞれメリット・デメリットがあります。
ロジスティック回帰
メリット
- 説明変数(特徴量)に対する重みを確認できるため、説明変数が多い場合に有効。
- ハイパーパラメーター調整が少なくて済み、かつ計算スピードが早いので扱いやすい。
デメリット
- 線形分離不可能なデータに弱い。
SVM(サポートベクターマシン)
メリット
- 説明変数(特徴量)が多い場合や少ない場合の両方に対応可能。
- 単純な問題に関してはNNよりも少ない教師データで、高い汎化性能を持てる。
- 計算が早く、過学習も起こしづらいため、使い勝手が良い。
デメリット
- サンプルの個数が100,000サンプルを超えるとうまく機能しない。
- データの前処理が必要(正規化や標準化)
k近傍法
メリット
- モデルが簡易的である。
- 事前の学習をせずに分析できる。
デメリット
- kの値によって予測が左右される。
- 訓練データが多いと、その分メモリが必要となり、計算コストがかかる。
- 大規模なデータには機能しずらい。
決定木
メリット
- 結果のモデルが容易に可視化可能で、専門家でなくても理解可能。
- データのスケールに対して完全に不変で、個々の特徴量は独立に処理され、データの分割はスケールに依存しないので、正規化や標準化が不要。
- 特徴量ごとにスケールが大きく異なるような場合でも二値特徴量と連続値特徴量が混ざっていても問題なく機能する。
- 「特徴量の重要度」がわかる。
デメリット
- 枝刈りを行っても過剰適合しやすく汎化性能が低い傾向がある。
まとめ
ここまで、教師あり学習の4つのアルゴリズムを見てきましたが、如何だったでしょうか。
教師あり学習とは、回帰や分類に使用する手法であり、「与えられるデータに対して予測・分類」を行っていきます。
4つのアルゴリズムのメリット・デメリットもまとめたので、ご自身で試したいときにぜひ参考にしてみてください。



 出典:
出典: